10151. Соревнование коров

n коров, пронумерованных от 1 до n, участвуют в соревновании по программированию. Как мы все знаем, одни коровы кодируют лучше, чем другие. Каждая корова имеет определенный постоянный рейтинг навыков, который уникален среди конкурентов.

Соревнование проводится в несколько раундов личных встреч, в каждом между двумя коровами. Если корова a имеет более высокий уровень навыков, чем корова b (1 ≤ a, b ≤ n, a ≠ b), то корова a всегда победит корову b.

Фермер Джон пытается ранжировать коров по уровню навыков. Имея список результатов m раундов с двумя коровами, определите количество коров, чей ранг можно точно определить по результатам. Гарантируется, что результаты раундов не будут противоречивыми.

Вход. Первая строка содержит два целых числа n (1 ≤ n ≤ 100) и m (1 ≤ m ≤ 4500). Каждая из следующих m строк содержит два целых числа которые описывают конкурсантов и результат (первым идет a – победитель) одного раунда соревнований: a и b.

Выход. Выведите единственное целое число, представляющее количество коров, чьи ранги можно определить.

Пример входа	Пример выхода
5 5 4 3 4 2 3 2 1 2 2 5	2

РЕШЕНИЕ

транзитивное замыкание

Анализ алгоритма

Объявим булевую матрицу g, где для каждой пары a и b установим g[a][b] = true, если корова a побеждает b (проведем ориентированное ребро от a к b). Известно, что результаты раундов не противоречивы, следовательно граф ациклический.

Ранг коровы с номером i можно определить, если для любой другой коровы j будет известно, что либо корова i может победить j (возможно через некоторых других), либо корова j может победить i. То есть в транзитивном замыкании графа должно выполняться либо g[i][j] = true, либо g[j][i] = true. Одновременно g[i][j] и g[j][i] равными true быть не могут, так как тогда данные будут противоречивы.

Пример

Для приведенного примера можно установить ранги только для коров 2 и 5. Корова 2 выиграет у 5, но проиграет всем остальным. Корова 5 проиграет всем.

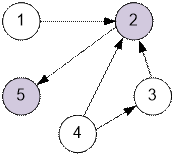
Для коровы 1 не известно, победит ли она коров 3 и 4. Соответственно для коров 3 и 4 не известно, победят ли они корову 1.

Реализация алгоритма

Объявим булевую матрицу g.

bool g[101][101];

Читаем входные данные.

scanf("%d %d", &n, &m);

Считаем что каждая корова побеждает саму себя.

for (i = 1; i <= n; i++) g[i][i] = 1;

Читаем входные данные. Строим входной граф.

for (i = 0; i < m; i++)

{

scanf("%d %d", &a, &b);

g[a][b] = 1;

}

Вычисляем транзитивное замыкание графа: если от вершины i до j существует путь по ребрам графа, то установим g[i][j] = true.

for (k = 1; k <= n; k++)

for (i = 1; i <= n; i++)

for (j = 1; j <= n; j++)

if (g[i][k] && g[k][j]) g[i][j] = true;

res = 0;

for (i = 1; i <= n; i++)

{

Установим, можно ли определить ранг коровы с номером i. Переберем всех коров j. Если для некоторой коровы g[i][j] = false и g[j][i] = false, то результат встречи коров i и j не определен и определить ранг коровы с номером i невозможно.

bool good = true;

for (j = 1; j <= n; j++)

if (g[i][j] == false && g[j][i] == false)

{

good = false;

break;

}

Если good = true, то ранг коровы с номером i можно установить.

if (good) res++;

}

Выводим ответ.

printf("%d\n", res);